Contributed by Tan Jing Long and Monica Chan  for SingTeach Virtual Staff Lounge

Computational thinking (CT) is poised to become de rigueur in schools. As it is, you may have heard of block-based programming such as Scratch or Micro:bit being used in the Applied Learning Programme (ALP) of some schools, featuring CT in its curricula.

What then is CT? CT is associated with the metacognitive aspect of computing, is closely related to mathematical thinking, and is more than just coding. Since CT encompasses a broad scope, a consensus is yet to be forged on the definition of CT.

Introduction to CT

CT can be considered the “connective tissue” between computer science and many traditional disciplines (Martin, 2018). For example, CT’s combination with classic STEM fields has produced new interdisciplinary fields such as computational geometry and bioinformatics (Lee et al., 2020). CT is a pedagogical and problem-solving method, where solutions can be expressed as algorithms (small computational steps) to be carried out by a computer (Aho 2012; Grover and Pea, 2013). Over the past decade across the world, CT has integrated into primary and secondary education, and has been promoted as an essential competence for every K-12 student (Grover and Pea, 2018).

Framework for CT

At the CTE-STEM conference, Peel and colleagues presented this CT taxonomy (2021), which we found particularly helpful in framing our ideas around CT implementation in Singapore:

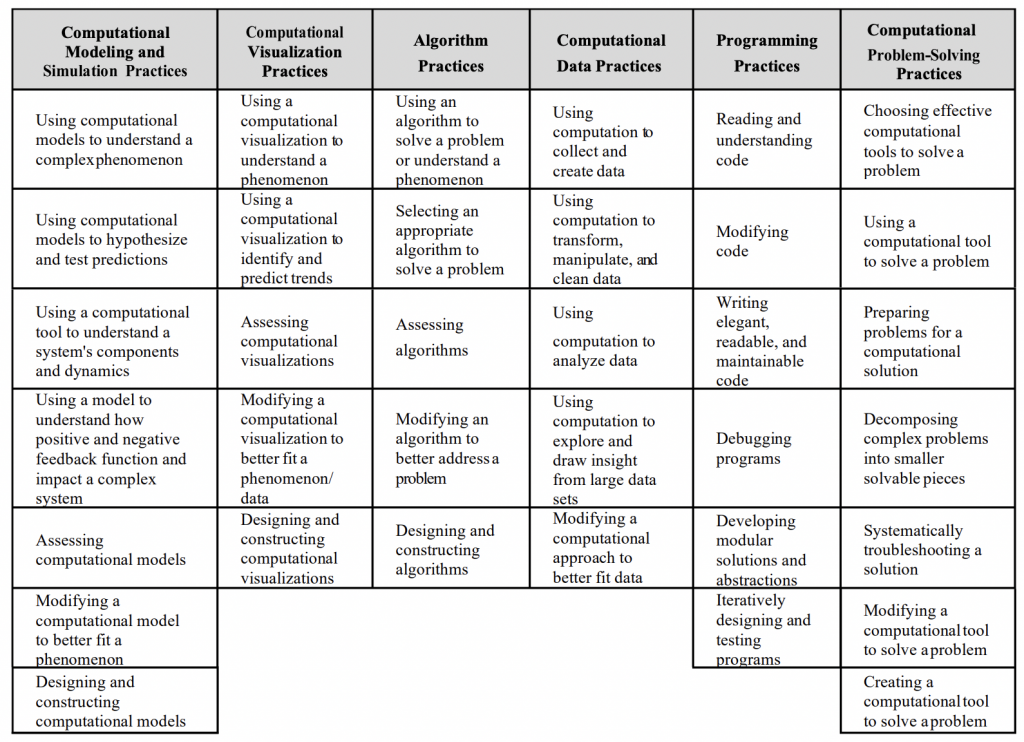
Figure 1. CT Taxonomy by Peel and colleagues (2021).

Computational models and simulations help students visualize a phenomenon, understand a system’s dynamics, and test predictions and hypotheses. Designing and constructing models help students form deeper understanding of phenomena (Wilensky & Reisman, 2006). NetLogo and PhET  are software built to perform accessible mathematical and scientific simulations.

Visualization is a metacognitive skill where students use graphs, tables, diagrams, static models and more to analyze and interpret data (Gilbert, 2005). Students may use a visualization to think about a phenomenon in different ways, especially when the visualization provides a new way of looking at the phenomenon.

Data practices include data collection, cleaning, transformation, and analysis, where students could use pre-programmed algorithms or write their own code to manipulate their data. Overlapping with data practices, programming is the act of writing code, which involves designing, debugging and testing. Students would also learn programming conventions such as using comments for code annotation.

Finally, for problem-solving, this requires students to understand various approaches to address a problem computationally, and to choose a suitable computational tool to solve the problem. Students may need to decompose problems into smaller pieces and manipulate the raw data to run an algorithm that solves the problem.

CT in Singapore

Beyond the Computing subject, the Ministry of Education, Singapore has recognized that CT ought to be inculcated in the compulsory curriculum, notably in math lessons. In Singapore, the Curriculum Planning and Development Division (CPDD) defines CT as follows:

Computational thinking can be described as the thought process involved in formulating problems and developing approaches to solving them in a manner that can be implemented with a computer (Wing, J. M., 2006). In general, CT refers to the ability to use four skills, namely – abstraction, decomposition, generalization and algorithmic thinking – in solving problems.

In a keynote speech at the CTE-STEM conference, A/Prof Ho Weng Kin exemplified how CT can be integrated seamlessly into the math curriculum, and shared a compelling success lesson from Singapore. A mathematician by training, A/Prof Ho (2021) chose the foremost but otherwise typically mundane topic: numerals. As the formal concept of rationality can be rather abstract and only accessible to more mathematically mature students, A/Prof Ho made the instructional decision to allow the students to build an intuition for irrational numbers by inductive discovery, using Microsoft Excel to iteratively “grow” their own irrational number. His success is perhaps accentuated by the irony in the students’ remarks: “If only every math lesson can be this fun.”

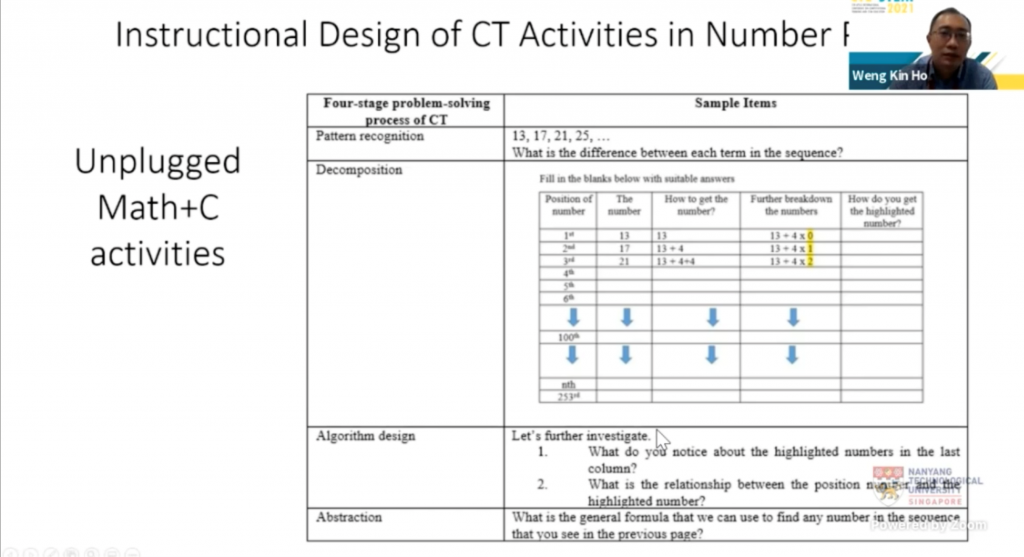
Figure 2. Screenshot of A/Prof Ho’s keynote address: Lesson Design for CT in Math.

Teachers’ Forum

Apart from the keynote, Day 3 of the conference was the highlight for teachers looking to bring home practicable ideas. The Teachers’ Forum saw educators from all around the region: India, Hong Kong, Indonesia, Thailand, Taiwan, China ­– each bringing to the table CT as it is in their respective sociocultural contexts. Mulyanto and colleagues (2021) assessed the impact of the internationally renowned Bebras Challenge and the Gerakan PANDAI, a homegrown movement to provide CT professional development to 22,000 elementary and junior high school teachers. It is striking how unplugged activities – that do not require a computer (including calculators) (Chang & Guo, 2021) – were creatively used in rural schools, where individual access to computers is a luxury. Palaparthi (2021) illustrated the implementation of CT in welfare schools in Andhra Pradesh, India, where students played algorithmic games to guess a birthdate, subconsciously invoking binary search.

Lee, Tang and Pang (2021) from the School of Science and Technology in Singapore engaged in a lesson study on integrating CT in math lessons. In this lesson, they taught 51 Secondary Two students of mixed to high ability the basic concepts of quadratic functions, with seven hours of Python programming training.

Figure 3. Screenshot of the SST sharing at the conference: Anchor CT Task.

In their work and written feedback, there was clear evidence that the students practised decomposition, and on occasion drew links between the different properties (pattern recognition) and relate the coefficients of the equation to the graph property directly (abstraction). Although not all groups were successful in providing complete code, the students demonstrated an understanding of the need of an algorithm and could relate aspects of algorithm design to mathematical techniques such as completing-the-square.

Math teachers will delight in Vizblocks, a data visualization literacy tool that an enterprising NUS undergraduate Travis Ching (2021) created, interoperable with Scratch.

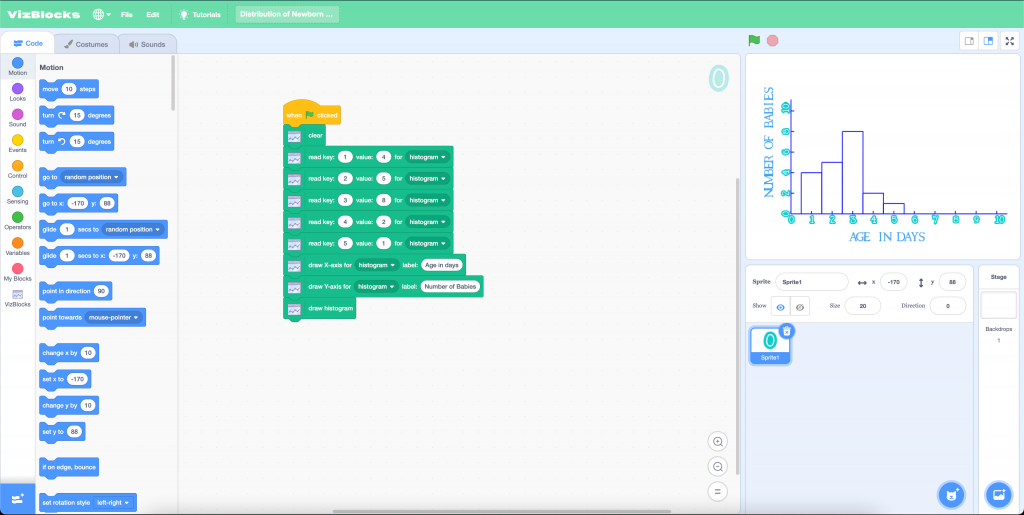
Figure 4. The user-interface of the Vizblocks platform. 

Vizblocks currently has eight visualizations, featuring many of the graphical representations concurrent in the math syllabus. As students are actively engaged in the construction process, they naturally become more conscious of key details of such graphs. For the teacher concerned about pedagogical support, Vizblocks also comes complete with teaching materials such as instructional slides and accompanying worksheets.

Conclusion

Taking a step back, you may be wondering (like we had), “Isn’t CT what we have been trying to do in problem-solving all along?” Indeed, there are strong parallels between CT and mathematical thinking, but with the distinguishing feature of computability, making for an authentic learning context.

If you are a math educator, we hope you are walking away a tad more inspired, and ever slightly more convinced on the importance of CT.

References

Aho, A. V. (2012). Computation and computational thinking. The computer journal, 55(7), 832-835.

Chang, J. & Guo, S. (2021). SWOT Analysis and Strategy of Unplugged Activities to Localize STEM Courses in Rural Schools. Proceedings of the 5th APSCE International Computational Thinking and STEM in Education Teachers Forum (CTE-STEM). Singapore: National Institute of Education.

Ching, T. J. Y., & Wadhwa, B. (2021). VizBlocks: A Data Visualization Literacy Education Tool. Proceedings of the 5th APSCE International Computational Thinking and STEM in Education Teachers Forum (CTE-STEM).  Singapore: National Institute of Education.

Gilbert, J. K. (2005). Visualization: A metacognitive skill in science and science education. In Visualization in science education (pp. 9-27). Springer, Dordrecht.

Grover, S., & Pea, R. (2013). Computational thinking in K–12: A review of the state of the field. Educational researcher, 42(1), 38-43.

Grover, S., & Pea, R. (2018). Computational thinking: A competency whose time has come. Computer science education: Perspectives on teaching and learning in school, 19.

Ho, W. K.  (2021).  Computational Thinking Through the Lens of a Mathematics Educator. Keynote presented at the 5th APSCE International Computational Thinking and STEM in Education Teachers Forum (CTE-STEM), Singapore.

Lee, I., Grover, S., Martin, F., Pillai, S., & Malyn-Smith, J. (2020). Computational thinking from a disciplinary perspective: Integrating computational thinking in K-12 science, technology, engineering, and mathematics education. Journal of Science Education and Technology, 29(1), 1-8.

Lee, T. Y. S., Tang, W. Q. J. & Pang, H. T. R. (2021). Computational Thinking in the Mathematics Classroom. Proceedings of the 5th APSCE International Computational Thinking and STEM in Education Teachers Forum (CTE-STEM).  Singapore: National Institute of Education.

Martin, F. (2018). Rethinking computational thinking. CSTA-The Advocate.

Mulyanto, A., Wisnubhadra, I. & Liem, I. (2021). Bebras Challenge and PANDAI Movement: Introducing Computational Thinking To K-12 Teachers in Indonesia. Proceedings of the 5th APSCE International Computational Thinking and STEM in Education Teachers Forum (CTE-STEM). Singapore: National Institute of Education.

Palaparthi, P (2021). Computational Thinking Implementation in Schools – An Experience with Rural Welfare Schools in India. Proceedings of the 5th APSCE International Computational Thinking and STEM in Education Teachers Forum (CTE-STEM).  Singapore: National Institute of Education.

Peel, A., Dabholkar, S., Wu, S., Horn, M.S., Wilensky, U. (2021). An Evolving Definition of Computational Thinking in Science and Mathematics Classrooms. Proceedings of the 5th APSCE International Computational Thinking and STEM in Education (CTE-STEM).

Wilensky, U., & Reisman, K. (2006). Thinking like a wolf, a sheep, or a firefly: Learning biology through constructing and testing computational theories—an embodied modeling approach. Cognition and instruction, 24(2), 171-209.