Why Singapore’s English Teachers Should Embrace Singlish, Not Fight It
Is it time for Singaporean educators to embrace Singlish as a legitimate learning tool? What the Research […]
Read More
Most secondary school students and teachers would be familiar with Science practicals. How about Math practicals? Could a “practical” lesson help us teach mathematical problem solving more effectively? A research project by NIE Math professors paves the way for this new approach.
Although Singaporean students do very well in Math internationally (as shown by the Trends in International Mathematics and Science Study [TIMSS]), they are relatively weaker on problem-solving items.
Attempts to teach problem-solving skills have not always met with success. Dr Toh Tin Lam and his colleagues at NIE believe that students are not motivated to learn as they are not assessed on this skill.
So, how can we teach problem solving effectively? A research project by Dr Toh and his team shows us how mathematical “practical” lessons could be the solution.
Mathematical problem solving is central to mathematics learning. It involves the acquisition and application of mathematics concepts and skills in a wide range of situations, including non-routine, open-ended and real-world problems. (MOE, 2006a, p. 6; MOE, 2006b, p. 2)
Mathematical problem solving is a core focus in Singapore’s primary and secondary math curriculum, in line with global trends in math education.
The ability to solve math problems is seen as a measure of spatial-logical cognitive ability. This means that if students successfully learn how to solve math problems, they will have learned how to think well.
The team used Polya’s model of problem solving (see Figure 1) as its 4-step approach is easy for the students to remember.
However, based on their previous experience, they expected that our students would be resistant to following the stages of the model. They found that even students who were able to solve the problems were reluctant to make the extra effort to check their work and extend the problem.
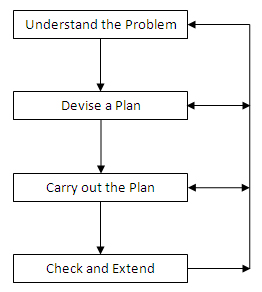
Figure 1. Flowchart of Polya’s problem-solving model.
To overcome this resistance, the team constructed a worksheet like that used in science practical lessons. Students were told to treat the lesson as a math “practical” lesson, and to follow the four steps closely.
The project team wanted to change the way students look at problem-solving work in class. By treating this as a “practical” lesson, they hoped students would accept problem solving as an integral part of math education, and not something that is difficult and irrelevant to them.
A problem-solving lesson has two parts.
For the first part, the students work on several problems while the teacher walks around the class to help and guide them. The teacher then works out the solutions with the class in a teacher-led discussion.
For the second part, the students work on the problem given in the worksheet. Students who cannot complete the problem in 15 minutes have to go through all four stages of Polya’s model. Students who are able to solve the problem within 15 minutes only have to do the last stage of the model.
This worksheet is especially useful for students who struggle to solve the problem as the specific questions at each stage (see box story) make them pause and be aware of their thought processes.
Encouraged by the success of the pilot project, the team was keen to explore how practical work can be extended to more math classrooms. They have recently embarked on a new research project called Mathematical Problem Solving for Everyone (M-ProSE).
The aim of the M-ProSE project is to design and implement a problem solving curriculum in Integrated Programme schools. The teachers will be trained on how to implement this curriculum in their classrooms and to assess its effectiveness.
By focusing on problem-solving skills, the team hopes to develop higher order thinking skills in our students. They are confident that these efforts will result in more engaged learners who are ready in the 21st century!
References
Ministry of Education. (2006a). Mathematics Syllabus Primary. Singapore: Ministry of Education, Curriculum Planning and Development Division. Retrieved March 25, 2009, from https://www.moe.edu.sg/education/syllabuses/sciences/files/maths-primary-2007.pdf
Ministry of Education. (2006b). Secondary Mathematics Syllabuses. Singapore: Ministry of Education, Curriculum Planning and Development Division. Retrieved March 25, 2009, from https://www.moe.edu.sg/education/syllabuses/sciences/files/maths-secondary.pdf
Toh, T. L., Quek, K. S., & Tay, E. G. (2008, December). Mathematical problem solving – A new paradigm. Paper presented at the Mathematical Association of Victoria Annual Conference, La Trobe University, Bundoora, Melbourne, Victoria, Australia.